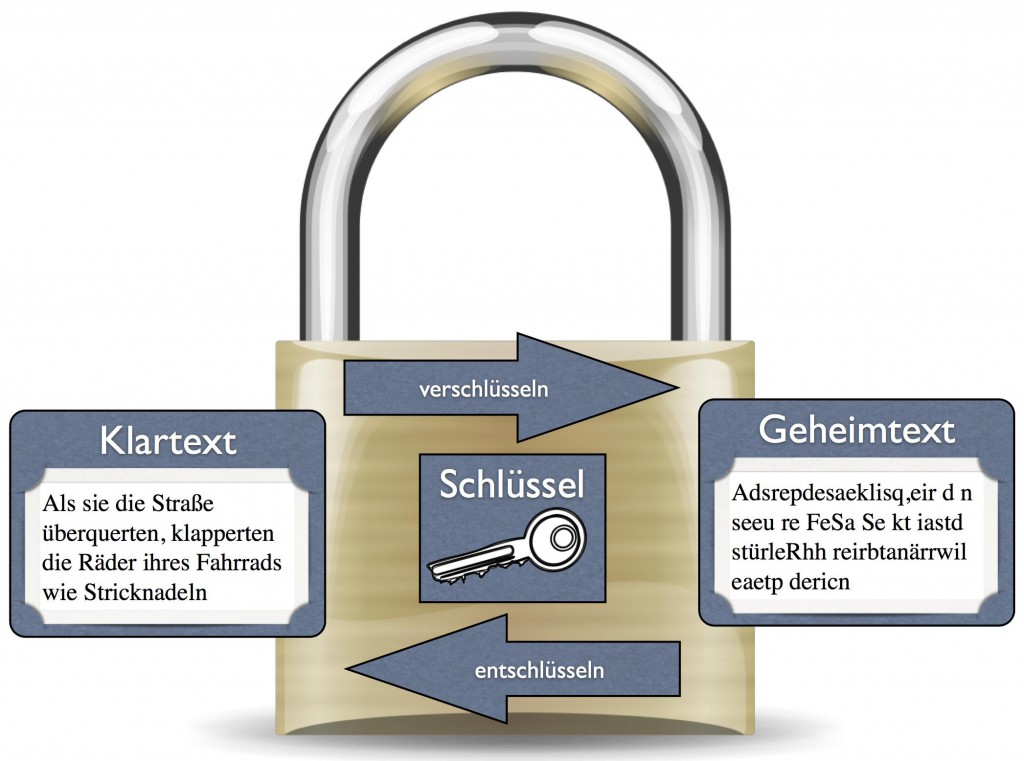
Die in den bisherigen Teilen behandelten Verfahren hatten alle eins gemein: Sender und Empfänger einer geheimen Nachricht mussten sich vor dem Versand auf einen gemeinsamen Schlüssel einigen, der auf einem sicheren Kanal übergeben werden musste. Es handelte sich um sogenannte symmetrische Verschlüsselungsverfahren.
Das funktioniert dann sehr gut, wenn wenige Personen, die zudem die Gelegenheit haben, Schlüssel persönlich zu tauschen, miteinander kommunizieren wollen. Im Internet dagegen funktioniert das so nicht. Wer eine verschlüsselte Webseite besucht, möchte Daten abhörsicher übetragen, hat aber normalerweise keine Gelegenheit dazu, mit dem Betreiber der Seite vor der eigentlichen Datenübertragung abhörsicher Schlüssel auszutauschen.
Mit der Entdeckung der Public-Key-Kryptographie Ende der 1970er Jahre wurde hier ein Durchbruch erzielt. Sogenannte asymmetrische Verschlüsselungsverfahren arbeiten mit zweigeteilten Schlüsseln. Der Schlüssel, der zum Chiffrieren einer Nachricht verwendet wird, ist ein anderer als der, mit dem die Nachricht wieder entschlüsselt werden kann. Da es mit ersterem Schlüssel nicht möglich ist, einen Geheimtext wieder zu dechiffrieren, braucht er auch nicht geheim gehalten zu werden. Nur der zweite Schlüssel muss geheim gehalten werden und nur der Empfänger muss ihn kennen, der Sender nicht. Es entfällt also die Notwendigkeit, einen gemeinsamen Schlüssel über einen sicheren Kanal auszutauschen, denn der öffentliche Schlüssel, der zum Verschlüsseln ausreicht, ist eben öffentlich und kann somit über den selben unsicheren Kanal ausgetauscht werden wie der Geheimtext!
Doch wie ist das möglich? Es gibt in der Mathematik sogenannte Einwegfunktionen. Diese haben die Eigenschaft, dass sie sich leicht berechnen lassen, ihre Umkehr jedoch nicht. Ein Beispiel dafür ist die Multiplikation zweier großer Primzahlen (leicht) und als Umkehr die Zerlegung des Produkts in seine Primfaktoren (schwer). Oder kurz: n = p * q lässt sich leicht berechnen, aber p und q lassen sich nicht direkt berechnen, wenn nur n bekannt ist. Allerdings gibt es eine Hintertür: Wenn man nicht nur die Zahl n kennt, sondern auch q, kann man p wieder leicht berechnen. Und auf einer Erweiterung genau auf dieses Prinzips basiert der 1978 vorgestellte RSA-Algorithmus.
Der RSA-Algorithmus hat wegen seiner Asymmetrie eine hohe praktische Relevanz bis heute. Doch bevor wir zur praktischen Anwendung kommen, zunächst noch ein klein wenig zum Hintergrund, wie der RSA-Algorithmus funktioniert, denn im Grund ist es gar nicht so schwer. mod ist dabei der Modulo-Operator, also der Rest einer ganzzahligen Division.
Vorbereitung:
1. Wähle zwei große Primzahlen p und q
2. Berechne n = p * q
3. Berechne ϕ(n) = (p-1)*(q-1)
4. Wähle e teilerfremd zu ϕ(n)
5. Bestimme d mit e*d mod ϕ(n) = 1
Öffentlicher Schlüssel: e und n
Privater Schlüssel: d
Verschlüsseln eines Klartextes m in Geheimtext c:
c = me mod n
Entschlüsseln eines Geheimtextes c in einen Klartext m:
m = cd mod n
Genauer kann man das noch unter anderem bei Beutelspacher [1] oder natürlich direkt bei den Entdeckern von RSA, den Herren Rivest, Shamir and Adleman, nachlesen [2]. Wie man erkennt, steht und fällt die Sicherheit dieses Verfahrens damit, dass man auch bei Kenntnis des Geheimtextes, des Klartextes und des öffentlichen Schlüssels nicht den privaten Schlüssel berechnen kann. Außerdem darf sich der Klartext nur mit Kenntnis des privaten Schlüssels aus dem Geheimtext berechnen lassen. Oder mathematisch gesagt: Auch, wenn man c, m, e und n kennt, kann man d nicht berechnen und wenn man c kennt, kann man m nur berechnen, wenn man auch d kennt. Wenn man jetzt noch etwas genauer schaut, dann sieht man, dass sich das alles berechnen ließe, könnte man die Zahl n, die ja Teil des öffentlichen Schlüssels ist, in ihre Primfaktoren p und q zerlegen. Sollte jemand also eine effektive Methode zur Primfaktorzerlegung großer Zahlen finden, wäre das RSA-Verfahren gebrochen.
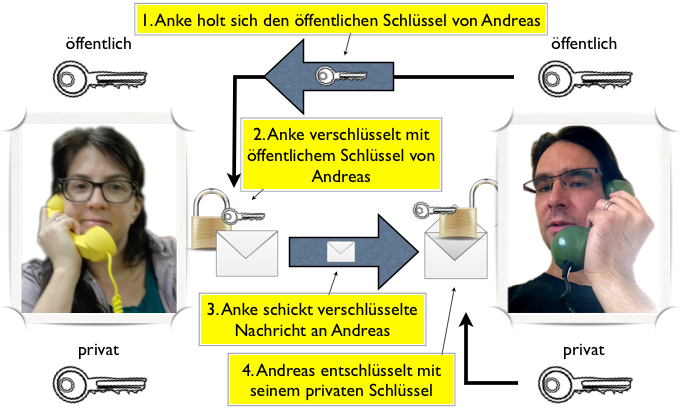
Mit sogenannten Public-Key-Verschlüsselungen wie RSA ist es also nun kein Problem mehr, auch mit Unbekannten verschlüsselt und abhörsicher zu kommunizieren. Das Problem des vorherigen Schlüsselaustauschs, das bei den symmetrischen Verschlüsselungsverfahren besteht, ist nun keins mehr. Der Ablauf der Kommunikation ist nun ganz einfach. Anke und Andreas haben jeweils zwei Schlüssel, einen öffentlichen und einen privaten. Der öffentliche Schlüssel kann allgemein bekannt gegeben werden. Möchte nun Anke eine verschlüsselte Nachricht an Andreas schicken, muss sie sich zunächst seinen öffentlichen Schlüssel besorgen. Den findet sie zum Beispiel auf seiner Webseite oder aber in einem Schlüsselverzeichnis im Internet, einem sogenannten Keyserver, der ähnlich wie ein Telefonbuch für das Nachschlagen von Personen, Mailadressen und dem dazu passenden Public Key erlaubt. Wenn Anke den öffentlichen Schlüssel von Andreas besorgt hat, benutzt sie diesen Schlüssel, um die Nachricht an Andreas zu verschlüsseln. Die verschlüsselte Nachricht schickt sie ab und nur Andreas kann sie wieder in Klartext verwandeln, weil nur er den passenden privaten Schlüssel hat.
Allerdings kommt nun ein anderes Problem neu hinzu: Wie kann Anke sicher sein, dass der öffentliche Schlüssel von Andreas wirklich ihm gehört und nicht heimlich von einem Bösewicht ersetzt wurde? Ein Angreifer, der in der Lage ist, sich zwischen die beiden zu schalten, könnte Anke seinen eigenen öffentlichen Schlüssel statt den von Andreas unterschieben, die Nachrichten mit seinem eigenen privaten Schlüssel entschlüsseln und mitlesen und zum Schluss mit Andreas‘ echtem öffentlichen Schlüssel wieder verschlüsseln und an ihn weiter schicken.
Diesen Angriff nennt man auch Man-in-the-Middle-Attack, weil der Angreifer zwischen den beiden legitimen Kommunikationspartnern sitzt. Doch warum ist dieser Angriff in der Praxis so gefährlich? Stellen wir uns vor, wir wollen Online-Banking betreiben und uns dabei einer verschlüsselten Verbindung bedienen. Wir können uns nun den öffentlichen Schlüssel der Bank besorgen und unsere Überweisungsdaten senden. Nur wer garantiert, dass wir wirklich mit der Bank direkt Verbindung aufgenommen haben und nicht mit einem Bösewicht, der uns vorgaukelt, die Bank zu sein? Um uns zu täuschen, könnte ein solcher Angreifer im Hintergrund unsere Anfrage an die Bank und die Antwort der Bank an uns durchleiten und nur mithören, um im entscheidenden Moment, wenn wir eine Überweisung tätigen, seine eigene Kontonummer und einen höheren Betrag einzusetzen.
Wir brauchen also eine Garantie, dass der öffentliche Schlüssel auch echt ist. Am einfachsten könnten Anke und Andreas diese Garantie bekommen, in dem sie über einen anderen Kanal, zum Beispiel am Telefon oder am besten persönlich, die öffentlichen Schlüssel (oder eine Prüfsumme davon, den sogenannten Fingerprint) vergleichen. Bei diesem Abgleich ist es nicht entscheidend, dass Anke und Andreas nicht abgehört werden, denn die dabei ausgetauschte Information ist ja nicht geheim. Es muss nur sichergestellt sein, dass ein Angreifer diese Information nicht verändern kann.

Praktischerweise können Public-Key-Verschlüsselungsalgorithmen wie RSA so „zweckentfremdet“ werden, dass sie nicht verschlüsseln, sondern stattdessen die Echtheit einer Nachricht garantieren! Man muss dazu eine Nachricht (oder eine Prüfsumme davon) mit seinem privaten Schlüssel verschlüsseln. Ein Empfänger kann die Nachricht dann mit dem öffentlichen Schlüssel des Absenders entschlüsseln. Wenn dabei der Klartext herauskommt, ist garantiert, dass die Nachricht tatsächlich unverändert vom Absender kommt, denn nur der Absender hat Kenntnis seines privaten Schlüssels und nur wenn die Nachricht damit verschlüsselt wurde, wird mit dem öffentlichen Schlüssel wieder der Klartext sichtbar.
Die asymmetrische Kryptographie wurde also gar nicht zur Verschlüsselung, sondern zur digitalen Signatur eingesetzt, die wie eine handschriftliche Unterschrift die Echtheit einer Nachricht garantiert.
Das ist schon mal gut, man kann also mit digitalen Signaturen die Authentizität und Integrität von Nachrichten prüfen, aber noch haben wir das ursprüngliche Problem nicht gelöst, da wir ja die Authentizität des öffentlichen Schlüssels an sich prüfen müssen!
Die Lösung besteht darin, dass eine dritte Stelle, der sowohl Anke als auch Andreas vertrauen, den öffentlichen Schlüssel von Andreas digital signiert. Man spricht dann auch davon, dass diese dritte Stelle durch diese Signatur ein Zertifikat erstellt hat, das die Echtheit garantiert. Wenn Anke den öffentlichen Schlüssel der Zertifizierungsstelle kennt, kann sie nun mit dem Zertifikat die Echtheit des öffentlichen Schlüssels von Andreas prüfen. Damit das funktioniert, muss aber immer noch der öffentliche Schlüssel der Zertifizierungsstelle sicher übertragen werden. Außerdem müssen, wie schon geschrieben, Anke und Andreas der Zertifizierungsstelle vertrauen, deswegen nennt man diese auch Trust Center. Bis jetzt klingt das erst mal so, als hätten wir durch die Einführung des Trust Centers noch nicht viel gewonnen, da wir ja immer noch einen öffentlichen Schlüssel, den des Trust Centers, haben, den wir vor unerlaubter Veränderung geschützt verteilen müssen. Wenn wir aber dieses Problem auf das Internet übertragen, so sehen wir, dass tatsächlich eine Vereinfachung eingetreten ist: Wir müssen nicht mehr für jede beliebige Webseite selbst prüfen, ob der öffentliche Schlüssel stimmt, wenn diese ein Zertifikat eines Trust Centers vorweisen kann. Die öffentlichen Schlüssel des Trust Centers bekommen wir schon mit dem Browser oder dem Betriebssystem mitgeliefert! Das Gesamtsystem mit Zertifizierungsstellen und Schlüsselverteilung nennt man auch Public-Key-Infrastruktur.
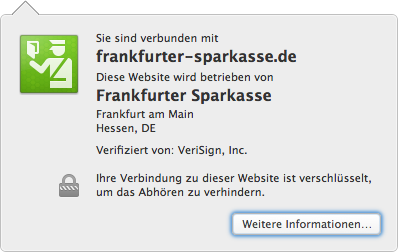
Wenn man mal bei einer Webseite, die mit HTTPS beginnt, auf der Adresszeile des Browsers an die richtige Stelle klickt, bekommen wir die wichtigsten Informationen eines solchen Zertifikats direkt angezeigt, wie hier zum Beispiel von der Frankfurter Sparkasse, deren öffentlicher Schlüssel in seiner Echtheit von der VeriSign Inc. bestätigt wurde.
Mit einem Klick auf „Weitere Informationen“ kann man noch viele Details erfahren, zum Beispiel welches genaue Verschlüsselungsverfahren verwendet wird, für welche Web-Adressen das Zertifikat genau gilt, wann es abläuft und so weiter. Es lohnt sich durchaus, sich das einmal genauer anzuschauen. Im übrigen wird die eigentliche Kommunikation symmetrisch verschlüsselt, mit dem asymmetrischen Verfahren wir nur ein temporärer Sitzungsschlüssel übertragen. Ein Grund dafür ist, dass Public-Key-Verfahren wie RSA sehr viel langsamer sind als symmetrische Verfahren wie das in der letzten Folge angesprochene AES. Außerdem sind sie anfälliger für bestimmte Arten von Angriffen. Man spricht von einem hybriden Kryptosystem, wenn symmetrische und asymmetrische Verfahren kombiniert werden.
Doch wo können wir nun Public-Key-Kryptographie einsetzen?
In der Praxis wird Public-Key-Kryptographie in der Variante wie beschrieben mit zentralen Zertifizierungsinstanzen (auch Certification Authority oder CA genannt) für sicheres Surfen im Web mit den Protokollen HTTPS bzw. SSL/TLS eingesetzt.
Für E-Mails gibt es das Protokoll S/MIME, das von den meisten Mailprogrammen unterstützt wird und ebenfalls auf von CAs signierte Zertfifikate setzt. Außerdem ist bei E-Mails das Protokoll PGP sehr weit verbreitet. Freie Implementierungen dieses Protokolls sind GnuPG bzw. Gpg4Win für Windows und GPGTools für den Mac. Wer Thunderbird als Mailprogramm verwendet, sollte sich das Plugin Enigmail anschauen. PGP basiert nicht auf zentralen CAs für die Echtheitsprüfung, stattdessen können Nutzer, die sich kennen, ihre öffentlichen Schlüssel gegenseitig signieren und somit selbst als Zertifizierungsinstanz für andere auftreten. Bei dieser dezentralen Public-Key-Infrastruktur spricht man vom Web-of-Trust.
Wer eine sichere Alternative zu SMS oder WhatsApp sucht, der sollte sich Threema anschauen. Anders als bei Apples iMessage, das laut Hersteller ebenfalls Ende-zu-Ende-Kryptographie verwendet, wird bei Threema der Schlüssel auf dem eigenen Endgerät erzeugt und nur der öffentliche Schlüssel zu einem Keyserver übertragen. Die Echtheit der Schlüssel kann bei einem persönlichen Kontakt über einen QR-Code verifiziert werden.
Ich kann nur jedem empfehlen, sich mit diesen Programmen zu beschäftigen und in Zukunft Mails und Kurznachrichten verschlüsselt zu versenden. Es tut nicht weh, ist innerhalb von ein paar Minuten eingerichtet und wer diesen Artikel bis hier gelesen hat, sollte die Grundprinzipien soweit verstanden haben.
Zum Abschluss in aller Kürze eine Zusammenfassung:
- Es gibt asymmetrische Verschlüsselungsverfahren mit öffentlichen Schlüsseln zum Chiffrieren und privaten Schlüsseln zum Dechriffrieren.
- Diese Systeme können auch für digitale Signaturen, also zur Prüfung von Authentizität und Integrität von Nachrichten, verwendet werden.
- Die privaten Schlüssel darf man niemals herausgeben.
- Bei öffentlichen Schlüsseln muss sichergestellt sein, dass sie wirklich zu dem Kommunikationspartner gehören, mit dem man Nachrichten austauschen möchte, sonst ist eine Man-in-the-Middle-Attack möglich. Die Prüfung kann durch von Zertifizierungsstellen ausgegebene Zertifikate geschehen.
- Die Verbindung ist nur sicher, wenn die Nachricht beim Sender verschlüsselt und beim Empfänger wieder entschlüsselt wird, die Nachricht also auf der ganzen Strecke verschlüsselt bleibt. Man spricht dann von Ende-zu-Ende-Kryptographie.
Mit diesem Teil ist meine kleine Serie über Kryptographie abgeschlossen. Ich hoffe, es hat allen Lesern Spaß gemacht, mir von den alten Griechen bis in die Neuzeit zu folgen und ein wenig zum Verständnis beigetragen. Ich hoffe auch, dass ich vielleicht ein paar von Euch dazu motivieren kann, sich mit PGP zu beschäftigen und in Zukunft verschlüsselte Mails zu verschicken, damit es die NSA nicht all zu leicht hat. Ich freue mich über Feedback und verschlüsselte Mails, mein Public Key ist auf meiner Homepage und wer mag, kann mir auch eine Nachricht über Threema auf mein Smartphone schicken!
Quellen und weiterführende Literatur:
[1] Albrecht Beutelspacher, Heike B. Neumann und Thomas Schwarzpaul: Kryptografie in Theorie und Praxis