In den Teilen 1 bis 4 waren historische Verschlüsselungsverfahren bis hin schreibmaschinenartigen, mechanischen Rotormaschinen, die etwa ab den 1920er Jahren im Einsatz waren, Thema. Dabei wurde aufgezeigt, dass zwar die besprochenen Verfahren (bis auf das One-Time-Pad) nicht sicher sind, aber viele Grundsätze heute noch Gültigkeit haben.

Zunächst wurden zwar mechanische Verschlüsselungsapparate noch bis in die 1970 Jahre eingesetzt und sogar für sicher gehalten, nicht zuletzt, weil von den Briten lange geheim gehalten wurde, dass die Enigma-Verschlüsselung gebrochen war. Aber natürlich mussten mit Aufkommen der Computertechnik neue Methoden gefunden werden. So wurde in den 1970er Jahren bei IBM die Entwicklung von Verschlüsselungsverfahren gestartet. Ein wichtiges Zwischenergebnis waren die von IBM-Mitarbeiter Horst Feistel entwickelten Feistel-Netzwerke.

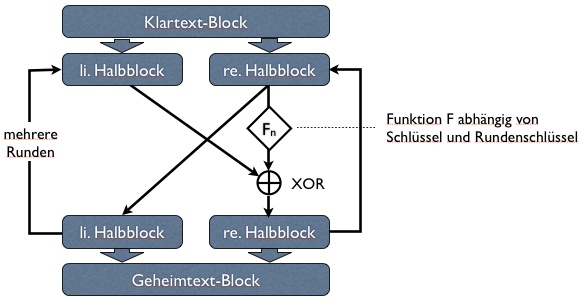
Bei einem Feistel-Netzwerk werden Blöcke von Bits über mehrere Runden hinweg nach folgendem Schema verschlüsselt: Zunächst wird eine Bitfolge in einen linken und rechten Halb-Block geteilt. Der rechte Halbblock wird direkt zum linken Halbblock der folgenden Runde. Außerdem dient der rechte Halbblock als Eingabe für eine Funktion, die vom Schlüssel und einem sogenannten Rundenschlüssel abhängt. Das Ergebnis dieser Funktion wird mit dem linken Halbblock exklusiv-oder-verknüpft und zum neuen rechten Halbblock. Diese Berechnung wird über mehrere Runden hinweg wiederholt. Die Rundenschlüssel sind für jede Runde verschieden und werden aus dem Schlüssel berechnet. Durch die Struktur des Netzwerks an sich ist sichergestellt, dass aus einem Geheimtext-Block mit Kenntnis des Schlüssels auch umgekehrt wieder der zugehörige Klartext-Block berechnet werden kann.

Ein Feistel-Netzwerk ist die Basis für den im Jahr 1976 veröffentlichen Data Encryption Standard (DES). Der DES-Algorithmus verschlüsselt Blöcke von 64 Bit Länge in 16 Runden mit Hilfe eines 56 Bit langen Schlüssels.

Die eigentliche Verschlüsselungsfunktion F (siehe Diagramm oben) ist etwas komplexer und basiert unter anderem auf einer fest definierten Substitution von Bitfolgen nach sogenannten S-Boxen, die in Abhängigkeit eines aus dem Schlüssel berechneten Rundenschlüssels ausgewählt werden. Eine genauere Beschreibung würde den Rahmen dieses Artikels sprengen, kann aber in der einschlägigen Literatur (siehe unten) oder auch im Wikipedia-Artikel zum Data Encrpytion Standard nachgelesen werden, denn wie alle guten Algorithmen ist auch der DES komplett offengelegt. Auch für die modernen Verfahren gilt nämlich selbstverständlich der Grundsatz, dass es keine Sicherheit durch Geheimhaltung des Verfahrens gibt („security through obscurity“), sondern dass nur der Schlüssel (und selbstverständlich der Klartext) geheim gehalten werden müssen.

Bei der Entwicklung war interessanterweise auch der heutzutage aus den Schlagzeilen bekannte US-Geheimdienst NSA beteiligt. Die NSA wollte eine kürzere Schlüssellänge, was ein Knacken der Verschlüsselung durch simples Ausprobieren aller möglichen Schlüssel („brute-force-Angriff“) natürlich vereinfacht. Aber abgesehen davon muss man davon ausgehen, dass die NSA nicht etwa versucht hat, durch Einflussnahme den Algorithmus zu schwächen. Vielmehr ist es so, dass die NSA bei den S-Boxen sogar die Resistenz gegen eine damals noch nicht öffentlich, wohl aber IBM und der NSA bekannte Art von Angriffen, der differentiellen Kryptanalyse, gesteigert hat.

DES gilt heute insbesondere wegen der für heutige Verhältnisse recht kurzen Schlüssellänge und der Weiterentwicklung der Technik nicht mehr als ausreichend sicher, allerdings wird die Variante „Triple-DES“ mit 112 Bit langen Schlüsseln noch stellenweise verwendet.

Der aktuelle Standard heißt AES, Advanced Encryption Standard. Der Algorithmus wurde 1998 unter dem Namen Rijndael (nach den Nachnamen seiner Entwickler Joan Daemen und Vincent Rijmen) entwickelt, setzte sich im Rahmen eines Wettbewerbs durch und wurde 2000 vom US National Institute of Standards and Technology (NIST). AES ist anders als DES kein Feistel-Netzwerk, sondern ein sogenanntes Substitutions-Permutations-Netzwerk. Der grundlegende Ablauf ist aber ähnlich: Es wird ein Block über mehrere Runden hinweg verschlüsselt und dabei S-Boxen (Substitution) und bei AES noch sogenannte P-Boxen (Permutation) verwendet.

AES verschlüsselt 128 Bit lange Blöcke, die Schlüssellänge beträgt 128, 192 oder 256 Bit und die Anzahl der Runden ist abhängig von der Schlüssellänge 10, 12 oder 14. Wie DES ist auch AES offengelegt, über einen langen Zeitraum hinweg von Wissenschaftlern öffentlich diskutiert, analysiert und für sicher befunden worden.

Da DES und AES jeweils Klartext-Blöcke verschlüsseln, spricht man auch von Blockchiffren. Streng genommen handelt es sich also dabei um eine monoalphabetische Substitution, nur dass nicht einzelne Zeichen (oder sagen wir 8 Bit-Blöcke), sondern längere Blöcke subsitutiert werden. Wird eine Blockchiffre so verwendet, spricht man vom ECB– oder Electronic-Codebook-Modus.

Tatsächlich ist es nun so, dass zwar statistische Angriffe, wie sie im zweiten und dritten Teil dieser Serie genannt wurden, zwar durch die längere Blockgröße (oder sagen wir das größere Alphabet) deutlich erschwert werden, aber je nach Klartext nicht völlig unmöglich gemacht werden. Insbesondere bei der Verschlüsselung von unkomprimierten Bilddateien werden Muster nur unzureichend verwischt, wie das Bildbeispiel bei Wikipedia eindrücklich zeigt.

Um diese Schwäche zu vermeiden, setzt man verkettete Verschlüsselungsmodi ein.

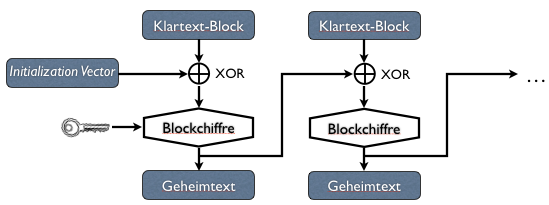
Vor der eigentlichen Verschlüsselung mit der Blockchiffre (also z.B. AES) wird der Klartext-Block mit dem vorhergehenden Geheimtext-Block exklusiv-oder-verknüpft. Da es beim ersten Block noch keinen vorhergehenden Geheimtext-Block gibt, wird stattdessen ein sogenannter Initialisierungsvektor verwendet, der als zusätzlicher Teil des Schlüssels aufgefasst werden kann. Diese Art der verketteten Verschlüsselung nennt man Cipher Block Chaining Mode oder kurz CBC.

Eine solche Verkettung kann auch auf andere Arten geschehen. Besondere Beachtung verdient dabei noch der Output Feedback Mode, kurz OFB.

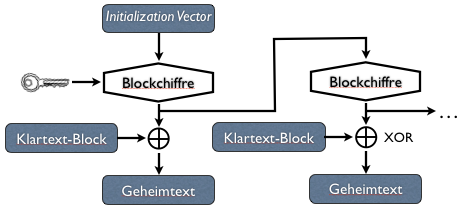
Das Bemerkenswerte hier ist, dass der Klartext gar nicht mit der Blockchiffre verschlüsselt wird! Schaut man sich das Schema einmal genauer an, stellt man fest, dass der eigentliche Verschlüsselungsalgorithmus ausschließlich dazu benutzt wird, eine Pseudo-Zufallszahlenfolge zu erzeugen, die dann mit dem Klartext exklusiv-oder-verknüpft wird. Dieses Vorgehen sollte aus dem dritten und vierten Teil dieser Serie bekannt vorkommen: Aus einem kurzen Schlüssel wird ein langer erzeugt, die eigentliche Verschlüsselung ist dann im Stil eines One-Time-Pads. Im Gegensatz zum echten One-Time-Pad ist aber keine absolute Sicherheit gegeben, da die erzeugte Bit-Folge ja nicht echt zufällig, sondern nur pseudo-zufällig ist.

Beachtenswert ist auch, dass zum Entschlüsseln eines mit einer Blockchiffre im OFB-Modus verschlüsselten Textes die Entschlüsselung der Blockchiffre gar nicht benötigt wird, sondern nur die Verschlüsselung. Die Blockchiffre dient schließlich nur dazu, eine Zufalls-Bitfolge zu erzeugen, die den Schlüssel für die eigentliche Ver- bzw. Entschlüsselung bildet.

Eine kleine Abwandlung des OFB ist der Cipher Feedback Mode CFB.

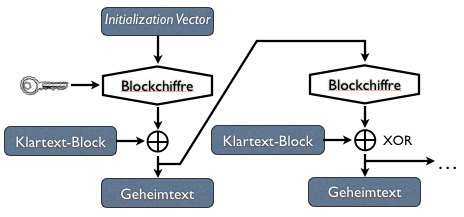
Vergleichen wir die drei bisher gezeigten Feedback-Modi, so stellt man folgendes fest: Beim OFB und beim CFB kommt der Klartext gar nicht mit dem eigentlichen Chiffrieralgorithmus in Berührung. Der Chiffrieralgorithmus dient in diesen Fällen nur dazu, eine Zufallszahlenfolge zu erzeugen und braucht auch gar nicht zu entschlüsseln. Es kann also statt einer echten Blockchiffre auch eine andere Einwegfunktion verwendet werden.

Beim CBC und CFB wird der Geheimtext als Feedback benutzt. Dies ist dann entscheidend, wenn auf dem Weg vom Sender zum Empfänger Datenblöcke verloren gehen. Beim OFB muss der Empfänger genau wissen, der wievielte Block gerade entschlüsselt werden soll. Beim CBC und CFB reicht es aus, den vorausgegangenen Geheimtextblock zu kennen, um ab diesem Punkt die Nachricht weiter entschlüsseln zu können.

Als letztes betrachten wir noch den Counter Mode (CTR).

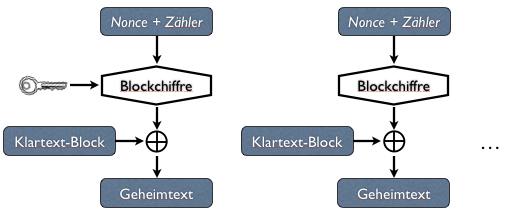
Statt eines Feedbacks wird dem Initialisierungsvektor (Nonce) lediglich ein Zähler hinzugefügt, aber wie beim CFB und OFB wird die Blockchiffre nur zur Erzeugung des eigentlichen Schlüssels verwendet. Der Vorteil gegenüber den anderen Verkettungsmodi besteht darin, dass alle Blöcke parallel verarbeitet werden können und entsprechend auch komplett unabhängig voneinander wieder dechiffriert werden können, wenn bekannt ist, um welchen Block es sich handelt.

Um den heutigen Artikel noch kurz zusammenzufassen: Die standardisierten Verschlüsselungsverfahren DES und der moderne AES sind sogenannte Blockchiffren, die Blöcke einer bestimmten Länge verschlüsseln und dafür mehrere Runden benötigen. Blockchiffren können entweder direkt blockweise im Electronic-Codebook-Modus verwendet werden, was aber nicht empfehlenswert ist, da Muster im Klartext ähnlich wie bei einer monoalphabetischen Chiffre nur unzureichend verwischt werden. Besser ist, einen verketteten Modus wie die hier gezeigten CBC, CFB, OFB oder CTR zu verwenden.

Die bisher gezeigten Verfahren haben alle die Eigenschaft, dass Sender und Empfänger einer verschlüsselten Nachricht vorher einen gemeinsamen Schlüssel getauscht haben müssen und nur mit Kenntnis des geheimen Schlüssels sowohl ver- als auch entschlüsselt werden kann. Wie man verschlüsselt kommunizieren kann, auch ohne dass man vorher persönlich einen Schlüssel ausgetauscht haben muss, werden wir in der nächsten Folge betrachten.

Quellen und weiterführende Literatur:

[1] Reinhard Wobst: “Abenteuer Kryptologie”